1.     Одинаковые маленькие металлические шарики, несущие одноименные заряды 15 и 60 нКл, находятся на расстоянии 2 м друг от друга. Шарики привели в соприкосновение. На какое расстояние их нужно развести, чтобы сила взаимодействия осталась прежней?

Так как шарики одинаковые, то после соприкосновения они будут иметь одинаковые заряды q’₁ = q’₂ = q’. По закону сохранения заряда

q₁ + q₂ = 2q’.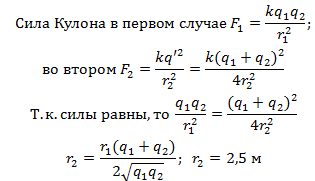

2.     Заряженные шарики, находящиеся на расстоянии 2 м друг от друга, отталкиваются с силой 1 Н. Общий заряд шариков 50 мкКл. Как распределен заряд между шариками?

Суммарный заряд шариков равен q = q₁ + q₂.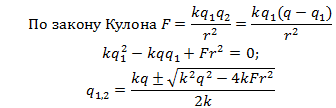

q₁ = 38 мкКл, q₂ = 12 мкКл. При вычислении корней системы уравнений получается, что q₁ = 12 мкКл, q₂ = 38 мкКл.

3.     Два маленьких одинаковых по размеру заряженных шарика, находящиеся на расстоянии 2 м, притягиваются с силой 27 мН. После того, как шарики приведены в соприкосновение и затем разнесены на прежнее расстояние, они стали отталкиваться с силой 9 мН. Определите первоначальные заряды шариков.

Так как шарики одинаковые, то после соприкосновения их заряды будут одинаковыми по модулю. Т.к. шарики до соприкосновения притягивались, то имели разноименные заряды; после соприкосновения отталкиваются, следовательно, заряды одноименные. Потому в законе сохранения заряда:

q₁ – q₂ = 2q’.

q = 4 мкКл

1)     q₂ = 6 мкКл                       2) q₂ = - 2 мкКл

q₁ = - 6 мкКл              q₁ = 2 мкКл

Т.о. q₁ = ± 6 мкКл, q₂ =  -+2 мкКл